Skip to content

MEV Risks

source

  • Call \(T_{MEV}\) the transaction fees netted by MEV transactions (in Gwei)
  • MEV transactions use an amount of gas \(g_{MEV}\)
  • Non-MEV transactions pay a miner fee \(\delta\) (in Gwei per gas unit)
  • Non-MEV transactions use \(g_N\) gas
  • The whole block (MEV + non-MEV) uses \(g = g_{MEV} + g_N\) gas
  • The block reward is \(R\) (in Gwei)
  • The uncle reward is \(U\) (in Gwei)
  • There is a rate \(p\) such that for each unit of gas added in the block, the uncle risk increases by \(p\). It was once measured that 10M gas adds about 2.5% risk, so we take \(p = 2.5 \times 10^{-9}\)

The expected revenue from a block including only MEV transactions is

\[ A = (1-pg*{MEV}) (R + T*{MEV}) + pg\_{MEV} U \]

The expected revenue from a block providing \(g\) gas in total is

\[ B = (1-pg) (R + T\_{MEV} + \delta g_N) + pgU \]

We look for \(\delta\) such that \(B \geq A\), which yields

\[ \delta \geq \frac{p(R + T\_{MEV} - U)}{1-pg} \]

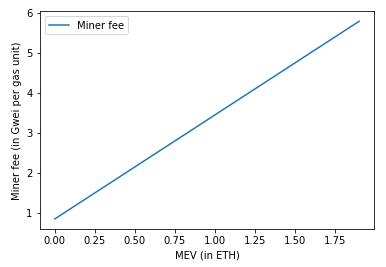
Note that this measure is independent of the quantity of gas used by MEV vs non-MEV transactions, but simply a function of the total gas used by the block \(g\). Calculating for \(T_{MEV} \in [0, 2 \times 10^9]\) (i.e., MEV in block netting between 0 and 2 ETH), we obtain the following values for \(\delta\), assuming 15 million gas is provided:

Recently, Tim Beiko argued that the value of \(p\) may be different:

> If we eyeball it, the gas limit goes from ~12.25m to ~14.75m, so +2.5m. In that, it seems like the uncle rates go from clustering around .045 to .049 (being somewhat generous), so a ~0.004 increase in uncle rate for a 2.5m increase. This means a 10m gas would add ~1.6% uncle risk, not 2.5% as your note assumes.

Note that as \(p\) decreases, so does the required miner fee.

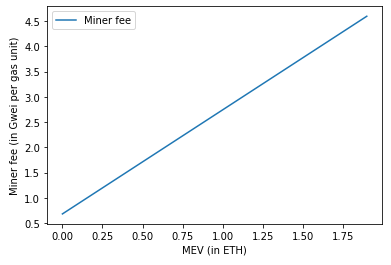With \(p = 2.0 \times 10^{-9}\)

Notebook source

How much MEV should I expect in the block?

See Flashbots mev-explore, reporting around 200 USD profit per bundle, i.e., ~0.1 ETH (@ 2000 ETH/USD).

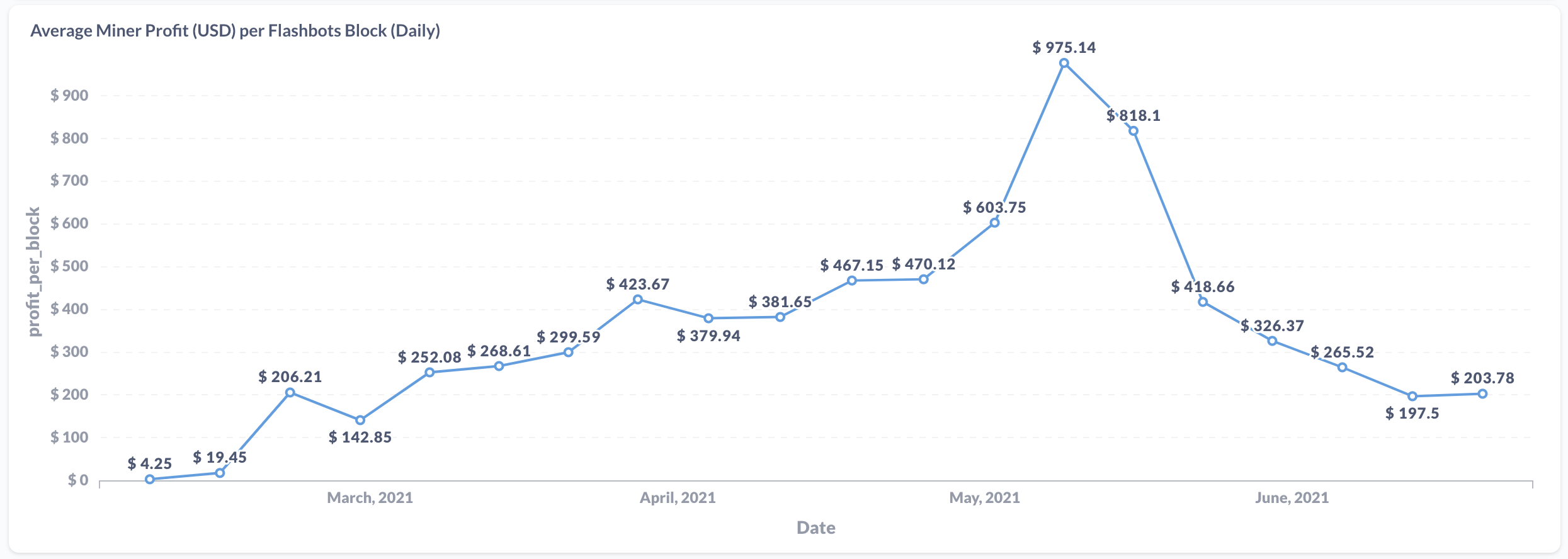
Note that since the above calculation is based on averages, there could be bundles netting much more than 0.1 ETH sometimes, and bundles netting much less than 0.1 ETH most times. A priority fee of ~2Gwei seems fine for most cases however.

Back to top